KMP定位子串
给定两个字符串S和B,定位B在S中的位置称之为串的模式匹配,其中S称之为主串,T为模式串。
1.朴素的模式匹配算法
一种很基础朴素的方法就是暴力匹配,采用定长顺序存储结构,不依赖于串的操作进行暴力匹配。
算法思想 :采用暴力匹配的方法,对主串和模式串设置i和j两个指针,从左到右一个一个进行匹配,当出现不匹配时,主串指针回溯,模式串从新开始进行匹配。
初始处理: 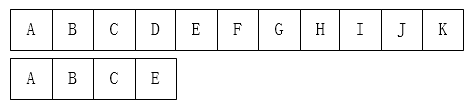
进行匹配: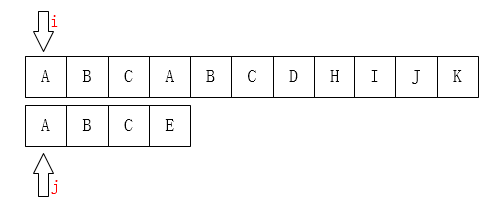
指针回溯: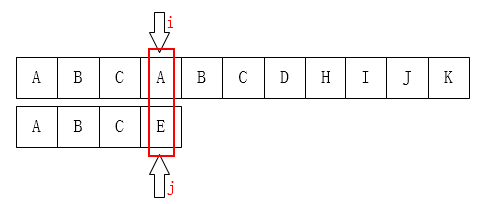
指针回溯: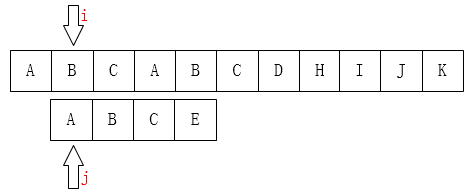
代码如下
int Index(String S,String T){
int i = 1,j = 1;
while(i <= S.len && j <= T.len){
if(S.ch[i] == T.ch[i]){ // 匹配则指针向前移动
++i;
++j;
}
else{
i = i - j + 2; //指针回溯
j = 1;
}
}
if(j > T.len)return i - T.len; //匹配成功返回第一个定位
return 0;
}
时间复杂度分析:分析最坏时间复杂度,如果主串前部分一直和模式串不能匹配,则指针会一直进行回溯,直到进行到最后的串,成功匹配,此时的时间复杂度取决于主串S和模式串T的长度n和m。时间复杂度为
2.KMP
很显然如果采用暴力算法,当主串和模式串不长的情况下,时间复杂度还算可行,但是一旦长度很�长,时间开销将会很大。于是三位大牛:D.E.Knuth、J.H.Morris和V.R.Prat一起发明了KMP算法,致力于解决这个主串指针回溯的问题来降低时间开销。KMP算法相对难度有点大,一开始学习半知不解,参考了一些博主的博文总结了一下这个算法。KMP算法详解-彻底清楚了(转载+部分原创) - sofu6 - 博客园 (cnblogs.com)
2.1 算法思想
算法思想:算法思想是按照我个人理解,KMP的核心就是基于朴素匹配算法,解决其主串指针回溯,从而降低时间开销。
过程描述对于S和T的匹配,当有相同部分,则指针将会向前移动,当出现不匹配时,是否有必要进行回溯呢?答案当然是否,因为对于主串来说,对于匹配的部分是已知信息,能否根据已知信息来判断模式串指针的下一步移动呢,从而达到降低时间复杂度的效果。由此,主串指针是不需要移动的,只需要根据已知信息来判断模式串的指针移动即可。 通过如下图片来感受下KMP的简化:
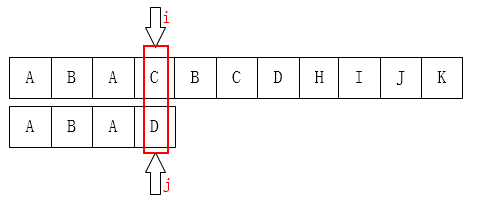
从上图发现当移动到C和D时,不匹配,肉眼观察,可以直接将j移动成如下的情况: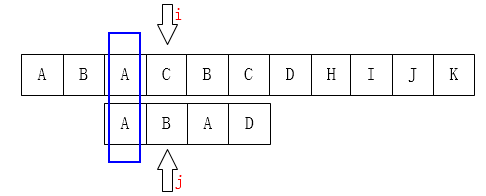
为什么呢?因为肉眼观察,前面的ABA是匹配的鸭!
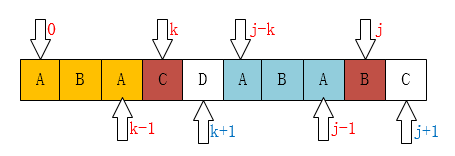
从上述的过程分析,我们可以发现当匹配失败时,j要移动的下一个位置k。存在着这样的性质:最前面的k个字符和j之前的最后k个字符是一样的。使用数学公式进行如下描述:
使用如下图片进行理解:
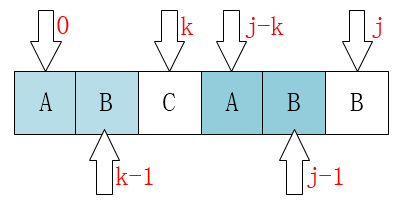
通过上述的分析,我们可以发现,进行匹配的过程中,对于主串的指针,是一往无前,无需回溯的,算法的核心在对于模式串的指针移动,当移动到不匹配的位置时候,需要进行计算,确定指针j的下一步走向。
2.2 next数组
接下来就是重点,我们现在知道了对于算法的核心就是当出现不匹配时候,我们的指针j要进行移动,那么j如何移动呢?根据模式串的特性,我们分析,这个移动跟主串无关,只跟模式串有关,我们需要一个next数组,来装载模式串不同位置上,对于出现不匹配时的指针下一步移动处理。next数组的重要意义就是,当出现不匹配时,模式串指针根据所在位置,进行下一步移动处理。下面介绍几种求解next数组的方法�。
1.王道老师的方法
根据课程的所给方法,我总结一下,该方法的相对直观,在手算中十分方便,目测观察,当主串和模式串出现不匹配时候,观察对于模式串指针,如何移动能使得在下一步匹配前,有较多模式串和主串已经匹配。如下图例,首先要初始化next数组,next数组的1和2无脑填0和1,不要问为什么,很明显,自己推一下即可:

当出现不匹配时候,在不匹配的前段,划一条竖线,观察模式串的指针j移动。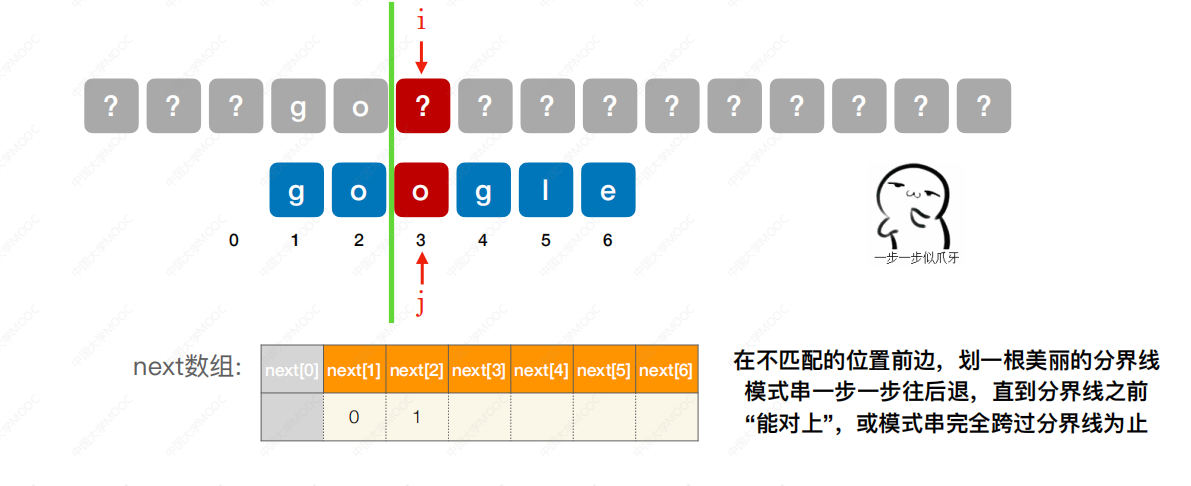
向前移动至2,o不匹配。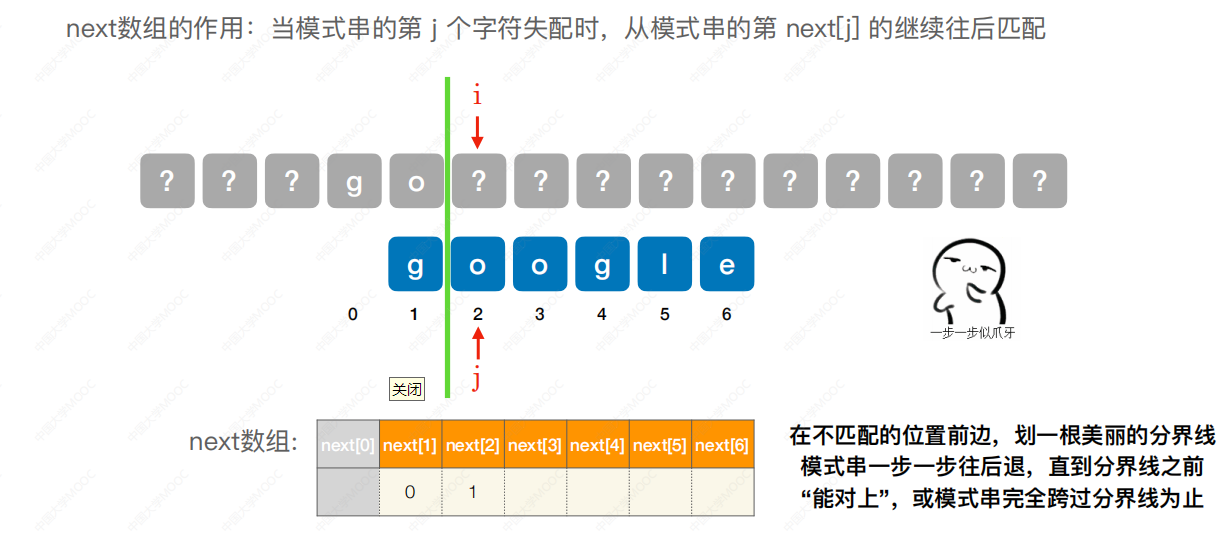
再向前移动到1,此时模式串next数组第一位是1,那么只能从这里进行下一步匹配(如果到0,那么0的会执行++,所以没有意义)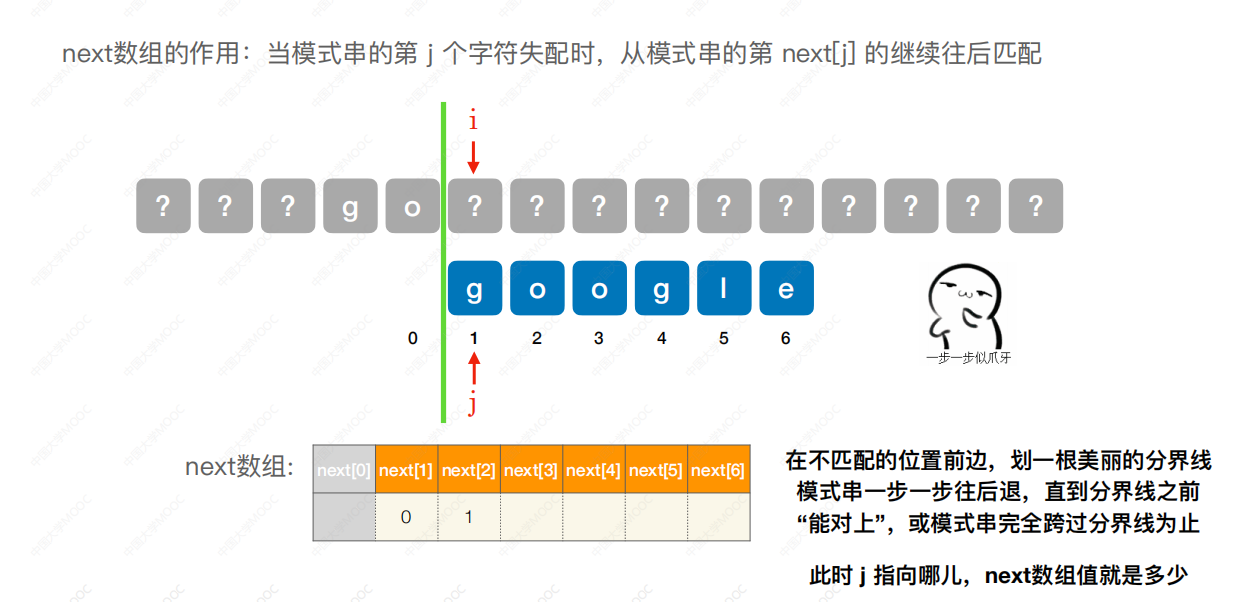
所以在next[3]处,我们填��写1,表示当出现到第三位不匹配时,下一步指针移动到1处。 后面的步骤都是依次类推,该方法适合手算next。
2.重复前后缀计算法
当我们匹配模式串和主串到一个不匹配的位置时候,我们要进行指针j的跳转。但是由于前面匹配的信息,我们可以发现
通过下图可以理解更透彻:
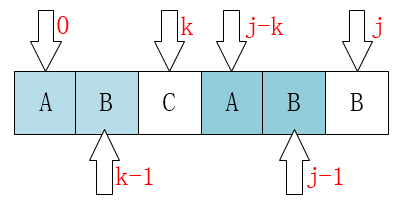
根据上图,当匹配到指针j的位置发现不匹配时候,我们肉眼观察到指针应该往k这个地方移动,为什么呢,因为显然前后的AB相等呀,而主串中指针扫过的位置,必有AB匹配,那么我们可以直接跳过前部的AB匹配。我们可以得出公式
上述公式就是我们求解next数组的核心思想。首先我们先来了解一下前后缀的概念,设一个字符串ababa,那么前缀就是除去最后一个a,然后从前往后看写出他的子集{a,ab,aba,abab}。同理后缀就是除掉第一个a,然后从后往前看写出子集{a,ba,aba,baba}。
接下来我们来模拟感受一下这个求解过程。首先next的1和2还是直接填0和1,没有为什么。 我们来看下图
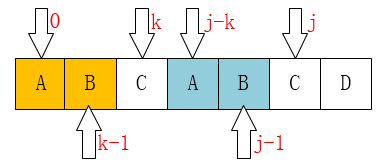
当模式串指针走到j时候,我们要计算next[j],记住next[j]跟j这个位置是什么没有关系,只跟前j-1个字符串有关。我们看前部分字符串,发现共同前后缀是AB,长度为2,那么意味着前两个字母和后两个字母是相同的,这时候的k指针自然就是指向3也就是C这个位置,为啥呢?因为从k指针开始作为区分��线,是不是前后相同?于是我们next[j]就填写为2。接下来再看,k指针和j指针的值相同,那么这时候我们要求解的是next[j],我们肉眼观察共同前后缀是不是ABC?长度为2,那么next[j+1]就是在next[j]的基础上加1即可,这个是可以递推出来的。我们发现如下规律
上述讨论的是当T[j] = T[k]的情况,那如果出现不相等的情况,如何处理呢?如下图
对于这种情况,我们执行。为什么呢?我们再来看下图:
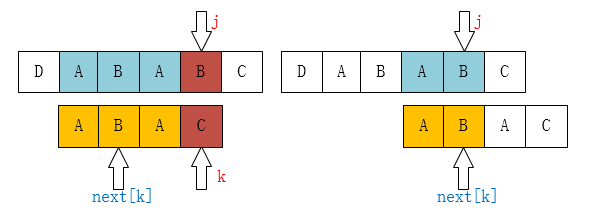
当到了时我们执行的目的是,寻找从k这个位置往前的最小前缀是否跟后面的最小后缀匹配。因为我们这个求解的核心就是找该指针之前的串的最大匹配的前后缀。当遇到不等的时候,也递推回去找更小的,当其中next[k]我们能明显的看出其值等于1,因为最长的前后缀长度为1,于是指针k指到了next[k]也就是B的位置,此时执行判定T[k]=T[j]?,如若相等就如上部分的情况,加1即可,如若不等则继续执行,一直递推下去,如果出现了k = next[k] = 1,那么此时下一步指针会走向0,意味着没有匹配的前后缀了,则该处会填写为0。 阅读文字难以理解,可以参考一个up主的讲解视频KMP算法之求next数组代码讲解_哔哩哔哩_bilibili。
2.3 求解代码
阅读到这里,next数组的求解就算结束了。我们来看下next数组的求解代码:
void get_next(String T,int next []){
int j = 1,k = 0;
next[1] = 0;
while(k<T.len){
if(k==0 ||T.ch[j] == T.ch[k]){ //如果相等
next[++j] = ++k; //next[j+1] = next[j] + 1
}
else{
k = next[k]; //回头寻找
}
}
}
KMP算法:
int Index_KMP(String S,String T,int next[]){
int i = 1;j = 1;
while(i<S.len && j<T.len){
if(j==0||S.ch[i] == T.ch[j]){
++i;
++j;
}
else{
j = next[j];
}
if(j>T.len) return i - T.len;
return 0;
}
}
2.4 next数组优化
仔细观察前述的图解跟代码,会发现,尽管主串指针不会回溯,但是模式串中的指针跳转重新匹配的过程中,会出现重复匹配失败的问题,从而浪费时间。例如下图:
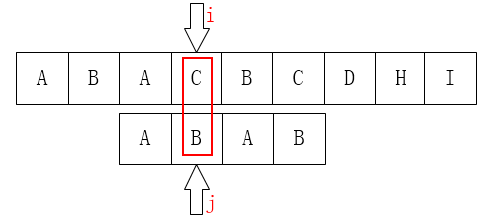
我们观察可以发现,匹配C和B时候会发现不匹配,此时的next会跳转到2,从AB再次匹配,但是通过第一次的不匹配我们可以得知的是,一定不会跟AB中的B进行匹配成功的,此时产生了一次无效匹配,然后next到1。
针对next数组进行优化,进行减少无效的匹配,提高效率。设计nextval数组来改善原next。基本思想就是遍历next数组,当跳转时候进行比较,如果T[next[j]]等于T[k],那么直接跳过这一层匹配,改为T[next[next[j]]即可。也就是跳过了中间无效的T[next[j]]和T[k]的比较。
代码实现
void get_nextval(String T,int nextval[]){
int j = 1,k = 0;
nextval[1] = 0;
while(j < T.len){
if(j == 0 || T.ch[j] == T.ch[k]){
++j;
++k;
if(T.ch[j] != T.ch[k]) nextval[j] = k; //不相等,则保留原有的最长重复前后缀
else nextval[j] = nextval[k]; //相等那就跳转,减少时间开销
}
else
k = nextval[k]
}
}